Greedy Algorithms with Sorting

• 青铜级（Bronze）- 贪心算法入门（Introduction to Greedy Algorithms）

  • 白银级（Silver）- 双指针法（Two Pointers）

• 核心内容：通过对输入进行排序来解决贪心问题

• 编程语言：C++

• 前置知识：

1. 参考资料（Resources）

通常，使用贪心算法时会存在一个“价值函数”，用于判断哪种选择是最优的。例如，我们常需要最大化或最小化某个量，因此会在下一步选择“价值最大”或“价值最小”的选项。

本模块将聚焦于“需要先对输入进行排序”的贪心问题。

2. 示例1 - 学习算法（Example - Studying Algorithms）

题目描述

斯蒂芬（Steph）想在寒假期间提升自己的算法知识。她总共有X（1 ≤ X ≤ 10^4）分钟的学习时间，有N（1 ≤ N ≤ 100）个算法需要学习，每个算法需要a_i（1 ≤ a_i ≤ 100）分钟才能掌握。求她最多能学会多少个算法。

• 题目来源：Problem - B - Codeforces

• 难度：极简单（Very Easy）

解决方案 - 学习算法（Solution - Studying Algorithms）

核心思路：斯蒂芬应优先学习“最简单”（即耗时最短）的算法，按所需时间从小到大依次选择，这样才能在有限时间内学会最多算法。

示例：

已知X = 15，N = 6，a_i = {4, 3, 8, 4, 7, 3}

将数组排序后得到{3, 3, 4, 4, 7, 8}

在15分钟内，斯蒂芬可学习前4个算法，总耗时3+3+4+4 = 14分钟，此时达到最大数量。

算法实现：

1. 对存储算法耗时的数组进行排序；

2. 依次累加数组元素，直到累加和超过X，统计累加的元素个数（即最多能学会的算法数量）。

时间复杂度：排序耗时O(N log N)，遍历数组耗时O(N)，总时间复杂度为O(N log N)。

C++代码：

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int X, N;
    cin >> X >> N;
    vector<int> algorithms(N);
    for (int i = 0; i < N; i++) {
        cin >> algorithms[i];
    }

    // 按耗时从小到大排序
    sort(algorithms.begin(), algorithms.end());

    int total_time = 0;  // 已使用的时间
    int count = 0;       // 已学会的算法数量
    for (int time : algorithms) {
        if (total_time + time <= X) {
            total_time += time;
            count++;
        } else {
            break;  // 时间不足，停止选择
        }
    }

    cout << count << endl;
    return 0;
}

3. 示例2 - 调度问题（Example - The Scheduling Problem）

题目描述

有N个事件，每个事件包含开始时间和结束时间。你同一时间只能参加一个事件，且一旦选择参加某个事件，必须全程参与。事件间的往返时间忽略不计。求最多能参加多少个事件。

• 题目来源：

• 难度：简单（Easy）

错误的贪心策略 - 选择最早开始的下一个事件（Bad Greedy - Earliest Starting Next Event）

一种直观的贪心思路是“始终选择最早开始的下一个事件”。红色的表示被选择的事件，以下为示例：

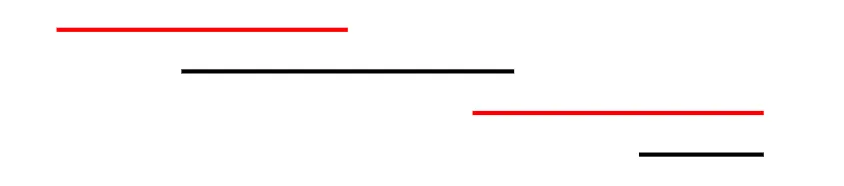
• 在某些情况下，该策略能得到最优解（如选择2个事件）；但在多数场景下会失效，例如：若某个事件开始早但持续时间极长，会导致无法参加后续多个短事件。

  

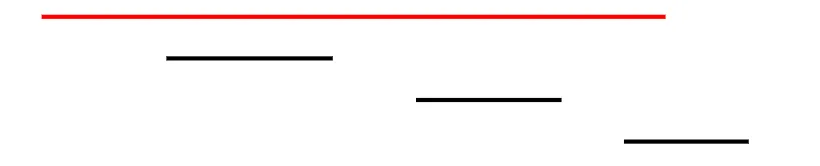
反例：选择最早开始的长事件后，仅能参加1个事件；而选择后续3个短事件，能参加3个事件，显然更优。

正确的贪心策略 - 选择最早结束的下一个事件（Correct Greedy - Earliest Ending Next Event）

正确的策略是“始终选择最早结束的下一个事件”，该策略能最大化后续可选择的事件数量。例如，在上述反例中，该策略可正确选择3个事件。

正确性证明

假设有两个事件E₁和E₂，其中E₂的结束时间晚于E₁。选择E₁始终是更优的，原因如下：

• 选择E₁后，剩余的时间更多，后续可选择的事件范围更大；

• 若存在一个事件能在E₂结束后参加，则该事件必然也能在E₁结束后参加（因E₁结束更早）；

• 即“可在E₂后参加的事件集合”是“可在E₁后参加的事件集合”的子集，因此选择E₁更优。

C++代码实现

使用C++的pair存储事件（为便于排序，存储格式为pair<结束时间, 开始时间>，因sort默认按pair的第一个元素排序）：

#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int N;
    cin >> N;
    vector<pair<int, int>> events(N);  // 存储格式：{结束时间, 开始时间}
    for (int i = 0; i < N; i++) {
        int start, end;
        cin >> start >> end;
        events[i] = {end, start};
    }

    // 按结束时间升序排序
    sort(events.begin(), events.end());

    int current_end = -1;  // 当前参加事件的结束时间（初始为-1，表示无已参加事件）
    int ans = 0;           // 最多能参加的事件数量

    for (auto &event : events) {
        int end = event.first;
        int start = event.second;
        // 若当前事件的开始时间 >= 上一个事件的结束时间，说明可参加
        if (start >= current_end) {
            current_end = end;
            ans++;
        }
    }

    cout << ans << endl;
    return 0;
}

4. 贪心算法的失效场景（When Greedy Fails）

以下将介绍几个贪心算法常见的失效场景，帮助避免在竞赛中陷入误区、浪费时间调试错误答案。

硬币找零（Coin Change）

问题描述：给定若干种硬币面额，求组成指定金额所需的最少硬币数量。

贪心算法的局限性：仅在特定场景下有效（如美国、欧元的硬币体系可证明贪心有效），但在通用场景下失效。

反例：

• 硬币面额：{1, 3, 4}

• 目标金额：6

• 贪心策略（选最大面额）：先选4，剩余2用两个1补充，共3枚硬币（{4, 1, 1}）；

• 最优解：选两个3，共2枚硬币（{3, 3}）。

显然，贪心策略得到的结果并非最优。

背包问题（Knapsack）

问题描述：给定若干物品，每个物品有重量和价值。选择部分物品装入背包，背包有最大重量限制，求装入物品的最大总价值。

反例：

• 背包最大容量：4

• 物品信息如下表：

• 贪心策略1（按价值从高到低）：选物品A（价值18，重量3），剩余重量1无法装下B或C，总价值18；

• 贪心策略2（按单位重量价值从高到低）：结果与策略1一致，总价值18；

• 最优解：选物品B和C（总重量4，总价值20），总价值更高。

结论：背包问题不存在有效的贪心解法，需使用动态规划（该知识点在黄金级（Gold）内容中覆盖）。

5. 练习题（Problems）

CSES 相关题目

其他来源题目（Other）