特别的问题（Ad Hoc Problems）

不属于具有成熟解决方案的标准类别的问题。

1. 引言

根据美国计算机奥林匹克竞赛（USACO）培训部分1.2的定义：

临时问题（Ad Hoc Problems）指其算法不属于具有成熟解决方案的标准类别的问题。每个临时问题都是独特的，不存在特定或通用的解决技巧。

以下是一些应对临时问题可能有用的通用建议：

绘制大量小案例以更好地理解问题。如果在调试时遇到困难，就多画案例；如果不知道如何着手解决问题，也多画案例。每当不知道如何进一步推进问题解决时，你很可能遗漏了重要的观察结论，因此请多绘制案例，并对问题的属性进行观察总结。
每当发现一个看似有用的观察结论，就把它写下来！记录想法能让你之后轻松回顾，也能确保不会忘记那些可能成为解决方案的思路。
不要拘泥于某一个特定想法，除非你能凭此看到完整的解决方案。
尝试从多个不同角度切入问题。可以试着摆弄公式，或者用可视化的方式呈现问题。解决临时问题时，最有帮助的做法之一就是不断尝试各种想法，直到取得进展。这是一种随着解题数量增多而会逐渐熟练的能力。
归根结底，提高解决临时问题（或任何类型问题）能力的最佳方法就是多做这类题目。

摄影作品2（Photoshoot 2）

难度等级：青铜级（Bronze）- 普通（Normal）

重点题目——请在继续阅读前尽力解决这道题！

答案：

如果该元素已处于目标位置，我们只需继续处理下一个元素。否则，若目标位置当前并未存在该元素，则我们通过将该元素标记为 “已移动” 并将答案（计数）加 1 来处理这种情况。

状态（Status）	来源（Source）	题目名称（Problem Name）	难度（Difficulty）	标签（Tags）	备注
（空）	http://oj.oldmoon.cn/p/U1516JB1	青铜级（Bronze）- 晋升计数（Promotion Counting）	简单（Easy）	（空）	（空）
（空）	http://oj.oldmoon.cn/p/U1819JB2	青铜级（Bronze）- 嗜睡奶牛排序（Sleepy Cow Sorting）	困难（Hard）	（空）	（空）
（空）	http://oj.oldmoon.cn/p/U1718FB3	青铜级（Bronze）- 驯服牛群（Taming the Herd）	困难（Hard）	（空）	（空）
（空）	http://oj.oldmoon.cn/p/U1617OB3	青铜级（Bronze）- 现代艺术（Modern Art）	困难（Hard）	（空）	（空）
（空）	http://oj.oldmoon.cn/p/U2021JS3	白银级（Silver）- 间隔排列（Spaced Out）	极难（Very Hard）	显示标签（Show Tags）：贪心算法（Greedy）	（空）

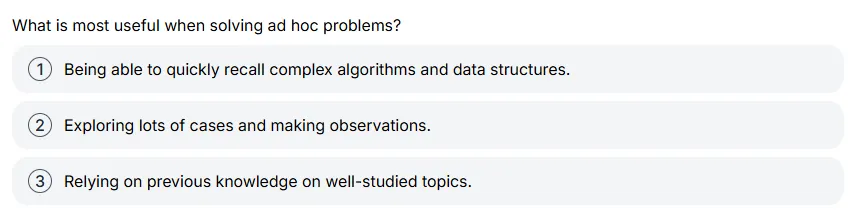
ans:2