Complete Search with Recursion
递归完全搜索(Complete Search with Recursion)
涉及遍历整个解空间的较难问题(包括需生成子集与排列的问题)
一、模块基础信息与定位
1. 核心定义
递归完全搜索是“完全搜索”的进阶形式,通过递归函数遍历整个解空间,适用于基础循环难以处理的场景(如生成子集、排列,或需要深度探索的问题),核心是“将大问题拆解为小问题,逐步探索所有可能”。
2. 青铜级定位
非必学但推荐:“递归知识对青铜级非严格必要”,但因内容更适配青铜级基础,故归入青铜模块(而非白银),掌握后可简化复杂搜索题的代码实现。
前置要求:需先掌握“基础完全搜索”(Bronze - Basic Complete Search),理解“遍历解空间”的核心思想。
3. 参考资源
模块内容参考多本经典算法资料,各小节具体资源见对应板块,核心参考包括:
CPH(《Competitive Programming Handbook》):子集、排列、回溯的代码与讲解。
CP2(《Competitive Programming 2》):迭代与递归完全搜索的对比。
二、子集生成(Subsets)
子集生成是递归完全搜索的基础场景,以“Apple Division(苹果分配)”为例,讲解两种生成子集的方法,例题难度为“CSES - Easy”(适配青铜级)。
1. 例题背景:Apple Division
有n个已知重量的苹果。你的任务是将这些苹果分成两组,使两组重量之间的差值最小。
输入
第一行输入一个整数n:表示苹果的数量。
第二行输入n个整数p₁、p₂、……、pₙ:分别表示每个苹果的重量。
输出
输出一个整数:即两组苹果重量的最小差值。
约束条件
1 ≤ n ≤ 20
1 ≤ pᵢ ≤ 10⁹
输入:
5
3 2 7 4 1
输出:
1
解释:
第一组苹果的重量为2、3和4(总重量9),第二组苹果的重量为1和7(总重量8)。
分析:
由于 n≤20,我们可以通过尝试将 n 个苹果划分为两组的所有可能方式,找到两组重量差值最小的方案。以下是两种实现方法。
2. 方法1:递归生成子集(Generating Subsets Recursively)
(1)实现逻辑
通过递归函数,对每个苹果做“二选一”决策:放入第一组(累加至 sum1)或放入第二组(累加至 sum2),直至遍历所有苹果(递归终止),返回当前分组的重量差。
递归参数:
index(当前处理的苹果索引)、sum1(第一组总重量)、sum2(第二组总重量)。终止条件:
index == n(所有苹果处理完毕),返回abs(sum1 - sum2)(当前分组的重量差)。递归过程:对每个
index,递归调用两种情况(苹果放入 sum1 或 sum2),取两种情况的最小差值作为当前结果。
(2)代码实现
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
int n;
vector<long long> weights;
// 递归函数:处理第index个苹果,返回最小重量差
ll recurse_apples(int index, ll sum1, ll sum2) {
// 终止条件:所有苹果处理完毕
if (index == n) {
return abs(sum1 - sum2);
}
// 递归两种选择:当前苹果放入sum1或sum2,取最小值
ll option1 = recurse_apples(index + 1, sum1 + weights[index], sum2);
ll option2 = recurse_apples(index + 1, sum1, sum2 + weights[index]);
return min(option1, option2);
}
int main() {
cin >> n;
weights.resize(n);
for (ll &w : weights) {
cin >> w;
}
// 初始调用:从第0个苹果开始,两组重量均为0
cout << recurse_apples(0, 0, 0) << endl;
return 0;
}3. 方法2:位掩码生成子集(Generating Subsets with Bitmasks)
此部分难度会超出铜级!
(1)核心概念
位掩码(Bitmask):用整数的二进制表示子集——若整数的第
i位为1,则第i个苹果属于第一组(s1);若为0,则属于第二组(s2)。遍历所有子集:
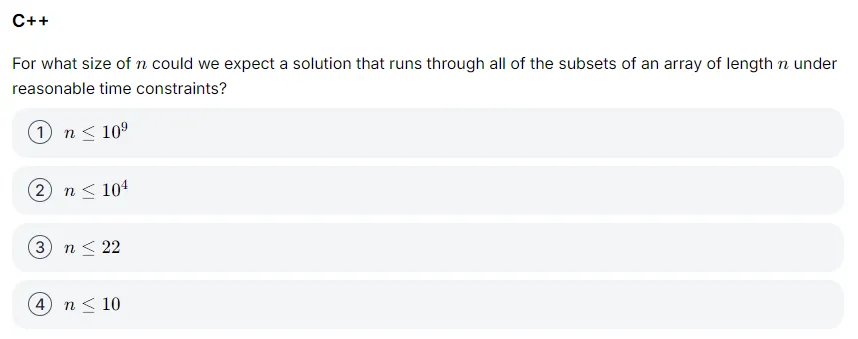
n个苹果的所有子集对应整数范围为0到2^n - 1(共2^n个子集),每个整数代表一种分组方式。
(2)示例(n=3)
整数(掩码) | 二进制 | 第一组(s1)包含的苹果索引 |
|---|---|---|
0 | 000 | {}(空集) |
1 | 001 | {0} |
2 | 010 | {1} |
3 | 011 | {0,1} |
4 | 100 | {2} |
5 | 101 | {0,2} |
6 | 110 | {1,2} |
7 | 111 | {0,1,2} |
(3)关键位运算
1 << x:等价于2^x,二进制表示为“第x位为 1,其余为 0”(用于定位第x位)。mask & (1 << x):判断掩码mask的第x位是否为 1——若结果为正,则第x位为 1(苹果x属于 s1);否则为 0(属于 s2)。
(4)代码实现
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
int main() {
int n;
cin >> n;
vector<ll> weights(n);
for (ll &w : weights) {
cin >> w;
}
ll total = accumulate(weights.begin(), weights.end(), 0LL);
ll min_diff = LLONG_MAX;
// 遍历所有掩码(0到2^n - 1)
for (int mask = 0; mask < (1 << n); ++mask) {
ll sum1 = 0;
// 计算当前掩码对应的s1重量和
for (int i = 0; i < n; ++i) {
if (mask & (1 << i)) {
sum1 += weights[i];
}
}
ll sum2 = total - sum1;
min_diff = min(min_diff, abs(sum1 - sum2));
}
cout << min_diff << endl;
return 0;
}(5)注意事项
青铜级不要求掌握位掩码,但该方法是子集生成的高效实现(代码简洁,无需递归栈,效率更高),建议作为进阶内容了解。
三、排列生成(Permutations)
排列是“元素的所有可能重排方式”,下面以“Creating Strings I(生成字符串排列)”为例,讲解递归生成和利用 STL 函数生成两种方法,例题难度为“CSES - Easy”。
1. 前置概念:字典序(Lexicographical Order)
(1)定义
排列的字典序与字典中单词的排序规则一致:
优先比较第一个元素,小的排列在前;
若第一个元素相同,比较第二个元素,以此类推;
若一个排列是另一个的前缀(如 [1,2] 和 [1,2,3]),则 shorter 的排列在前。
(2)示例(3个元素的排列,按字典序)
[1,2,3] → [1,3,2] → [2,1,3] → [2,3,1] → [3,1,2] → [3,2,1]
(3)应用场景
题目若要求“按字典序输出所有排列”,需确保生成顺序符合规则;
若仅需“遍历所有排列”,则无需严格遵循字典序,但需了解该概念(青铜级题目如“Photoshoot”会涉及)。
2. 例题背景:Creating Strings I
题目描述
给定一个字符串,你的任务是生成所有可由其字符组成的不同字符串。
输入
仅一行输入,为一个长度为n的字符串,每个字符均在a–z之间。
输出
首先输出一个整数k:表示可生成的不同字符串的数量。随后输出k行,每行一个字符串,且所有字符串按字母顺序(词典序)排列。
约束条件
1 ≤ n ≤ 8
输入
aabac
输出
20 aaabc aaacb aabac aabca aacab aacba abaac abaca abcaa acaab acaba acbaa baaac baaca bacaa bcaaa caaab caaba cabaa cbaaa
3. 方法1:递归生成排列(Generating Permutations Recursively)
(1)实现逻辑
状态记录:用
char_count[26]记录每个字符的剩余数量(避免重复排列),用curr记录当前正在构建的排列。递归过程:对每个剩余字符(
char_count[c] > 0),将其加入curr,减少对应字符的计数,递归调用;递归返回后,恢复字符计数(回溯)。终止条件:
curr.size() == s.size()(当前排列长度等于原字符串长度),将curr加入结果列表。
(2)代码实现
#include <bits/stdc++.h>
using namespace std;
string s;
vector<string> perms;
int char_count[26] = {0}; // 记录每个字符的剩余数量
// 递归函数:构建当前排列curr
void search(const string &curr = "") {
// 终止条件:当前排列完成
if (curr.size() == s.size()) {
perms.push_back(curr);
return;
}
// 遍历所有可能的字符
for (int c = 0; c < 26; ++c) {
if (char_count[c] > 0) {
// 选择当前字符
char_count[c]--;
search(curr + (char)('a' + c));
// 回溯:恢复字符数量
char_count[c]++;
}
}
}
int main() {
cin >> s;
// 初始化字符计数
for (char ch : s) {
char_count[ch - 'a']++;
}
// 递归生成所有排列
search();
// 输出结果(已按字典序,因递归时按a-z顺序选择字符)
for (const string &p : perms) {
cout << p << endl;
}
return 0;
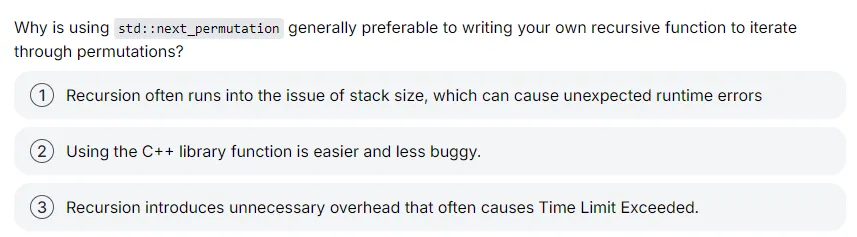
}4. 方法2:利用 STL 的 next_permutation 函数
(1)函数特性
next_permutation(v.begin(), v.end()):将容器v调整为“下一个字典序更大的排列”,返回true;若已为最大排列(如 [3,2,1]),返回false。使用要求:需先将容器排序(按字典序从小到大),否则会遗漏比初始排列小的排列。
循环结构:用
do-while循环(而非while),确保初始排列(最小排列)被处理。
(2)代码实现
#include <bits/stdc++.h>
using namespace std;
int main() {
string s;
cin >> s;
sort(s.begin(), s.end()); // 排序,确保从最小字典序开始
vector<string> perms;
do {
perms.push_back(s); // 处理当前排列
} while (next_permutation(s.begin(), s.end())); // 生成下一个排列
// 输出所有排列(已去重,因next_permutation自动跳过重复)
for (const string &p : perms) {
cout << p << endl;
}
return 0;
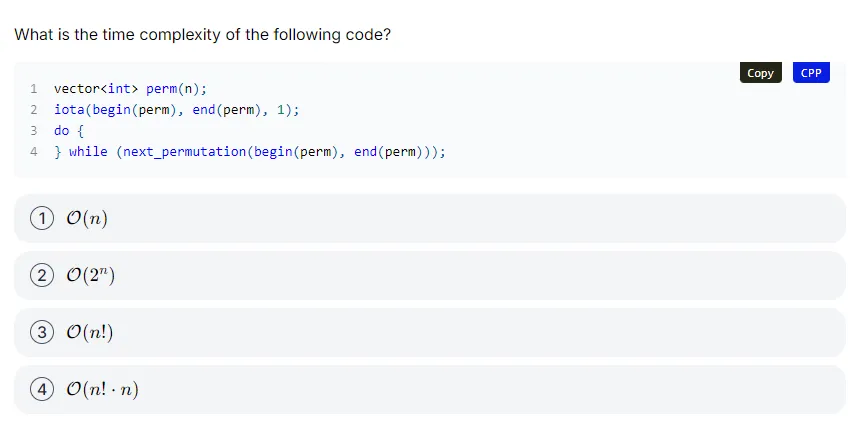
}(3)时间复杂度
若遍历 n 个元素的所有排列(共 n! 个),每次 next_permutation 平均执行 O(n) 次交换,故总时间复杂度为 O(n! * n)。
四、回溯法(Backtracking)
回溯法是“递归搜索 + 剪枝”的进阶形式,通过“尝试-回溯-再尝试”的过程,避免无效搜索,以“Chessboard & Queens(棋盘与皇后)”为例,讲解两种回溯实现,例题难度为“CSES - Normal”。
1. 例题背景:Chessboard & Queens
https://www.luogu.com.cn/problem/P1219
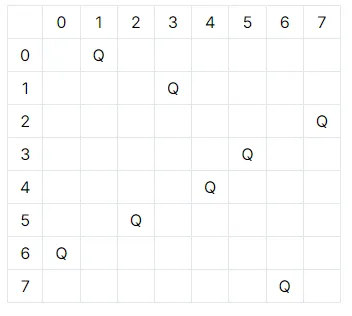
问题描述:在 8x8 棋盘上放置 8 个皇后,要求:① 皇后不互相攻击(不同行、不同列、不同对角线);② 避开棋盘上的障碍格子,求合法放置方案数。
核心思路:通过回溯法逐步放置皇后,实时检查合法性,避免无效尝试。
2. 方法1:基于排列的回溯(By Generating Permutations)
(1)优化逻辑
降维简化:因皇后不同列,可将“列”作为索引,“行”作为值——用排列
perm[col] = row表示“第col列的皇后放在第row行”,确保不同行、不同列。左下到右上对角线:同一对角线上的格子满足
row + col = 常数;右下到左上对角线:同一对角线上的格子满足
row - col = 常数;对每个排列,检查皇后是否在同一对角线,且不在障碍格子上。
减少解空间:8 列皇后的排列共
8! = 40320种,远少于暴力枚举的C(64,8)(约 40 亿种),大幅提升效率。对角线检查:
(2)代码实现(核心片段)
#include <bits/stdc++.h>
using namespace std;
const int DIM = 8;
vector<vector<bool>> blocked(DIM, vector<bool>(DIM)); // 标记障碍格子
// 检查排列是否合法(皇后不共对角线,且不在障碍格)
bool is_valid(const vector<int> &perm) {
unordered_set<int> diag1, diag2; // 记录已使用的对角线
for (int col = 0; col < DIM; ++col) {
int row = perm[col];
// 检查障碍
if (blocked[row][col]) return false;
// 检查对角线
int d1 = row + col;
int d2 = row - col;
if (diag1.count(d1) || diag2.count(d2)) return false;
diag1.insert(d1);
diag2.insert(d2);
}
return true;
}
int main() {
// 读取障碍格子('*'表示障碍)
for (int r = 0; r < DIM; ++r) {
string row;
cin >> row;
for (int c = 0; c < DIM; ++c) {
blocked[r][c] = (row[c] == '*');
}
}
// 初始化排列:perm[col] = row(0~7)
vector<int> perm(DIM);
iota(perm.begin(), perm.end(), 0); // 初始为[0,1,2,...,7]
int count = 0;
// 遍历所有排列
do {
if (is_valid(perm)) {
count++;
}
} while (next_permutation(perm.begin(), perm.end()));
cout << count << endl;
return 0;
}3. 方法2:标准回溯法(Using Backtracking)
(1)实现逻辑
状态记录:
rows_taken[row]:标记第row行是否已放皇后;diag1[d]:标记“左下到右上”对角线d是否已放皇后(d = row + col);diag2[d]:标记“右下到左上”对角线d是否已放皇后(d = row - col + DIM - 1,避免负索引);
递归过程:按列依次放置皇后(
col从 0 到 7),对每个列,尝试所有合法行(不在障碍格、行未被占、对角线未被占),放置后更新状态,递归处理下一列;递归返回后,恢复状态(回溯)。终止条件:
col == DIM(所有列均放置皇后),方案数加 1。
(2)代码实现
#include <bits/stdc++.h>
using namespace std;
const int DIM = 8;
vector<vector<bool>> blocked(DIM, vector<bool>(DIM));
vector<bool> rows_taken(DIM, false); // 标记行是否被占用
vector<bool> diag1(2 * DIM - 1, false); // 左下到右上对角线(row+col)
vector<bool> diag2(2 * DIM - 1, false); // 右下到左上对角线(row-col + DIM-1)
int count = 0; // 合法方案数
// 回溯函数:处理第col列
void backtrack(int col) {
// 终止条件:所有列已处理
if (col == DIM) {
count++;
return;
}
// 尝试在当前列的每一行放置皇后
for (int row = 0; row < DIM; ++row) {
// 检查合法性:不在障碍格、行未占、对角线未占
if (blocked[row][col]) continue;
int d1 = row + col;
int d2 = row - col + DIM - 1; // 调整为非负索引
if (rows_taken[row] || diag1[d1] || diag2[d2]) continue;
// 放置皇后,更新状态
rows_taken[row] = true;
diag1[d1] = true;
diag2[d2] = true;
// 递归处理下一列
backtrack(col + 1);
// 回溯:恢复状态
rows_taken[row] = false;
diag1[d1] = false;
diag2[d2] = false;
}
}
int main() {
// 读取障碍格子
for (int r = 0; r < DIM; ++r) {
string row;
cin >> row;
for (int c = 0; c < DIM; ++c) {
blocked[r][c] = (row[c] == '*');
}
}
// 从第0列开始回溯
backtrack(0);
cout << count << endl;
return 0;
}五、练习题模块
8 道递归完全搜索相关练习题,按难度分为“Normal(中等)”“Hard(难)”“Very Hard(极难)”,覆盖子集、排列、回溯三大场景:
难度等级 | 来源 | 题目名称 | 核心考点 | 解题关键 |
|---|---|---|---|---|
Normal(*) | Air Cownditioning II | 子集生成、递归 | 枚举所有空调的开启组合,计算是否满足温度需求,记录最小成本。 | |
Normal(*) | Livestock Lineup | 排列生成、递归 | 生成所有动物的排列,筛选符合“相邻约束”(如A必须在B旁边)的排列。 | |
Normal | Back and Forth | 递归搜索 | 模拟两个谷仓之间的往返运输,记录所有可能的最终库存,统计不同值的数量。 | |
Normal | CCC | Twenty-four | 排列生成 | 生成4个数字的所有排列和运算符组合,判断是否能得到24。 |
Normal | CSES | Beautiful Permutation II | 排列生成 | 生成满足“恰好k个相邻元素差为1”的排列。 |
Hard | CF | Three Logos | 子集生成、排列 | 枚举三个logo的摆放方式(旋转、位置),判断是否能恰好填满矩形。 |
Very Hard | Bronze | Printing Sequences | 递归搜索 | 按特定规则生成序列(如无连续重复元素),统计符合条件的序列数量。 |
六、测验:时间复杂度判断