图论入门

引言

图可用于表示多种事物，从图像到无线信号皆可，但最简单的类比是地图。想象一张包含多个城市且城市间有双向道路连接的地图，与图相关的问题包括：

城市A与城市B是否相连？将“区域”定义为一组城市，组内任意城市均可到达组内其他所有城市，但无法到达组外城市。这张地图中有多少个这样的区域？每个区域包含哪些城市？（USACO白银级题目类型）
从城市A到城市B的最短行驶距离是多少？（USACO黄金级题目类型）

对于USACO青铜级而言，只需掌握图的基本表示方法（通常是邻接表）即可。


计算机科学导论（CSA）	图论入门（Introduction to Graphs）	交互式
计算机科学导论（CSA）	图的表示（Graph Representations）	交互式 - 邻接表与邻接矩阵
计算机科学导论（CSA）	图编辑器（Graph Editor）	可用于可视化自定义图形
《算法竞赛入门》（CPH）	11 - 图论基础（Basics of Graphs）	图论术语、图的表示
IUSACO	10.1至10.3 - 图论（Graph Theory）	图论基础、图的表示、树
PAPS	6.4 - 图论（Graphs）	邻接矩阵、邻接表、映射

构建邻接表

图作为输入时，通常采用以下格式：

第一行包含节点数N和边数M。
接下来M行，每行包含一对整数，表示图中的一条边。

例如，计算机科学导论（CSA）资源中给出的无向图，其输入表示如下：

该图可在计算机科学导论（CSA）的图编辑器中可视化：

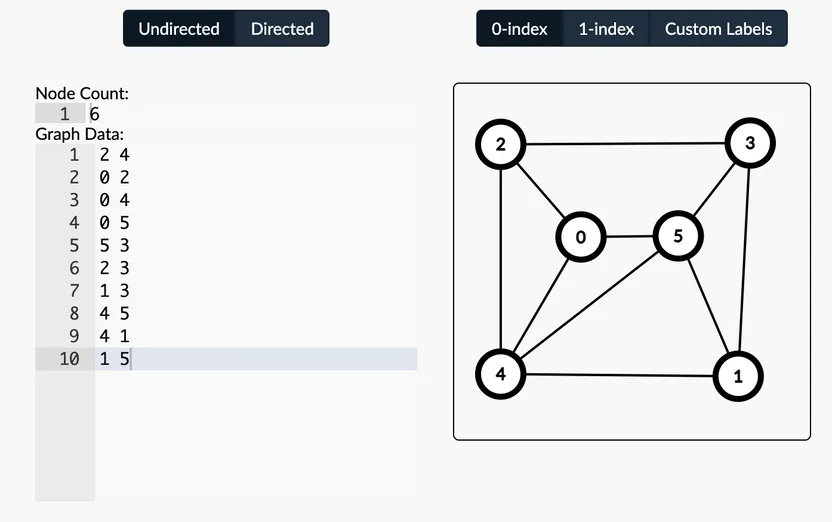
以下代码使用邻接表表示该图。将图转化为这种表示形式后，很容易统计某个节点的邻居数量，或遍历某个节点的所有邻居。

#include <iostream>
#include <vector>
using namespace std;

int main() {
	int N, M;
	cin >> N >> M;
	vector<vector<int>> adj(N);
	for (int i = 0; i < M; ++i) {
		int u, v;
		cin >> u >> v;
		adj.at(u).push_back(v);
		adj.at(v).push_back(u);
	}
	{
		int u = 1;
		// print number of vertices adjacent to u
		cout << "deg(u) = " << adj.at(u).size() << endl;
		// print all edges with u as an endpoint
		for (int v : adj.at(u)) cout << "{" << u << ", " << v << "}" << "\n";
	}
}

输出（Output）：

deg(u) = 3
{1, 3}
{1, 4}
{1, 5}

青铜级图论题目是什么样的？

以下所有题目至少属于以下两类之一：

1. 图的结构具有特殊性（是树、路径或环）。

2. 解决问题只需遍历每个顶点的邻接表。

此外，掌握白银级图论主题的知识通常会对解题有帮助，但并非解决青铜级图论题目的严格要求。

牲畜排队（Livestock Lineup）

青铜级 - 困难

该题的预设解法是通过暴力枚举所有可能的奶牛排列，时间复杂度为$\mathcal{O}(N\cdot C!)$，但如果我们用图来表示题目中的约束条件，可在$\mathcal{O}(C)$的时间复杂度内解决该问题。

基于图的解决方案

警告！

本解释及后续实现均假设输入中的所有约束条件描述的是不同的奶牛对。若该假设不成立，需先移除重复的约束条件。

注意，由于输入保证有效，最终我们总能得到若干“奶牛链”，且可按任意方式排列这些链。以题目中的示例为例，我们会得到如下“链”表示：

链（Chains）

需注意，对于未参与任何链的奶牛，在实现时可将其视为长度为1的独立链。

基于这种表示方法，我们可按字典序（字母顺序）遍历所有奶牛。当访问到可能是某条链起点的奶牛（即该奶牛最多有一个必填邻居）时，反复遍历其邻居，将访问到的奶牛加入排列序列，直到到达链的终点。

实现

时间复杂度：$\mathcal{O}(C)$

	#include <algorithm>
#include <fstream>
#include <map>
#include <string>
#include <vector>

using std::endl;
using std::string;
using std::vector;

Code Snippet: Cow Names (Click to expand)

int main() {
	std::map<string, int> cow_inds;
	for (int i = 0; i < COWS.size(); i++) { cow_inds[COWS[i]] = i; }

	std::ifstream read("lineup.in");
	int req_num;
	read >> req_num;
	vector<vector<int>> neighbors(COWS.size());
	for (int r = 0; r < req_num; r++) {
		string cow1;
		string cow2;
		string trash;
		read >> cow1 >> trash >> trash >> trash >> trash >> cow2;

		// Convert the names to their index in the list
		int c1 = cow_inds[cow1];
		int c2 = cow_inds[cow2];
		neighbors[c1].push_back(c2);
		neighbors[c2].push_back(c1);
	}

	vector<int> order;
	vector<bool> added(COWS.size());
	for (int c = 0; c < COWS.size(); c++) {
		if (!added[c] && neighbors[c].size() <= 1) {
			added[c] = true;
			order.push_back(c);

			if (neighbors[c].size() == 1) {
				int prev = c;
				int at = neighbors[c][0];
				while (neighbors[at].size() == 2) {
					added[at] = true;
					order.push_back(at);

					int a = neighbors[at][0];
					int b = neighbors[at][1];
					int temp_at = a == prev ? b : a;
					prev = at;
					at = temp_at;
				}
				added[at] = true;
				order.push_back(at);
			}
		}
	}

	std::ofstream out("lineup.out");
	for (int c : order) { out << COWS[c] << endl; }

自我检测

状态（STATUS）	来源（SOURCE）	题目名称（PROBLEM NAME）	难度（DIFFICULTY）	标签（TAGS）
http://oj.oldmoon.cn/p/U1819FB2	Bronze	The Great Revegetation	Hard	Show Tags
http://oj.oldmoon.cn/p/U1819OB2	Bronze	★ Milk Factory	Hard	Show Tags
http://oj.oldmoon.cn/p/U1718FB2	Bronze	Hoofball	Hard	Show Tags
http://oj.oldmoon.cn/p/U1920FB3	Bronze	Swapity Swap	Hard	Show Tags
http://oj.oldmoon.cn/p/U1819OB3	Bronze	Cow Evolution	Very Hard	Show Tags
	Bronze	Family Tree	Very Hard	Show Tags