二分查找（Binary Search）

核心内容：对任意单调函数进行二分查找
编程语言：C++
前置知识：白银级（Silver）- 有序数组的二分查找（Binary Search on a Sorted Array）

1. 引言（Introduction）

参考资料（Resources）

二分查找的核心逻辑：首先确定一个包含答案的搜索区间（大小为N），然后在每一轮迭代中将搜索区间缩小一半，因此算法只需验证O(log N)个值。这种方式效率极高，远优于遍历搜索区间内所有可能值的方法。

2. 单调函数的二分查找（Binary Search on Monotonic Functions）

假设存在一个布尔函数f(x)。在这类问题中，我们通常需要找到满足f(x) = true的最大x或最小x。与“有序数组的二分查找”类似，“基于答案的二分查找”仅在答案函数具有单调性（即函数始终非递增或始终非递减）时成立。

3. 寻找满足

我们需要构造一个函数lastTrue，使得lastTrue(lo, hi, f)返回区间[lo, hi]内满足f(x) = true的最后一个x。若不存在这样的x，则返回lo - 1。

只有当f(x)满足以下两个条件时，才能通过二分查找实现该功能：

1. 若f(x) = true，则对所有y ≤ x，均有f(y) = true；

2. 若f(x) = false，则对所有y ≥ x，均有f(y) = false。

示例：若f(x)的取值如下：

f(1) = true、f(2) = true、f(3) = true、f(4) = true、f(5) = true
f(6) = false、f(7) = false、f(8) = false

则lastTrue(1, 8, f) = 5，lastTrue(7, 8, f) = 6（注：因7-8区间内无满足f(x)=true的x，故返回7-1=6）。

实现方式1（Implementation 1）

需验证此实现不会在[lo, hi]区间外调用f(x)。

#include <bits/stdc++.h>
using namespace std;

int last_true(int lo, int hi, function<bool(int)> f) {
    // 若区间内无满足条件的x，返回lo - 1
    lo--;
    while (lo < hi) {
        // 计算当前区间的中点（向上取整）
        int mid = lo + (hi - lo + 1) / 2;
        if (f(mid)) {
            // 若f(mid)为true，说明更大的x可能满足条件，将左边界更新为mid
            lo = mid;
        } else {
            // 若f(mid)为false，说明满足条件的x在左侧，将右边界更新为mid - 1
            hi = mid - 1;
        }
    }
    return lo;
}

若不熟悉主函数中使用的语法，可参考“Lambda表达式（Lambda Expressions）”相关内容。

实现方式2（Implementation 2）

该方法基于“区间跳跃（interval jumping）”：从区间起始位置开始，通过跳跃缩小范围，且跳跃长度随接近目标值而减小。跳跃长度采用2的幂次，与“二进制跳跃（Binary Jumping）”原理相似。

#include <bits/stdc++.h>
using namespace std;

int last_true(int lo, int hi, function<bool(int)> f) {
    lo--;
    // 初始跳跃长度为区间总长度，每次迭代将跳跃长度减半
    for (int dif = hi - lo; dif > 0; dif /= 2) {
        // 若跳跃后位置仍在区间内且满足f(x)=true，更新左边界
        while (lo + dif <= hi && f(lo + dif)) {
            lo += dif;
        }
    }
    return lo;
}

4. 寻找满足

我们需要构造一个函数firstTrue，使得firstTrue(lo, hi, f)返回区间[lo, hi]内满足f(x) = true的第一个x。若不存在这样的x，则返回hi + 1。

与前一部分类似，仅当f(x)满足以下两个条件时，才能通过二分查找实现：

1. 若f(x) = true，则对所有y ≥ x，均有f(y) = true；

2. 若f(x) = false，则对所有y ≤ x，均有f(y) = false。

实现逻辑与“寻找最大x”类似，但满足条件时需缩小右边界，不满足时缩小左边界：

#include <bits/stdc++.h>
using namespace std;

int first_true(int lo, int hi, function<bool(int)> f) {
    hi++;
    while (lo < hi) {
        int mid = lo + (hi - lo) / 2;
        if (f(mid)) {
            // 若f(mid)为true，说明更小的x可能满足条件，将右边界更新为mid
            hi = mid;
        } else {
            // 若f(mid)为false，说明满足条件的x在右侧，将左边界更新为mid + 1
            lo = mid + 1;
        }
    }
    return lo;
}

5. 示例 - 最大中位数（Example - Maximum Median）

题目来源：Div 2 C - Maximum Median
难度：CF - 简单（Easy）

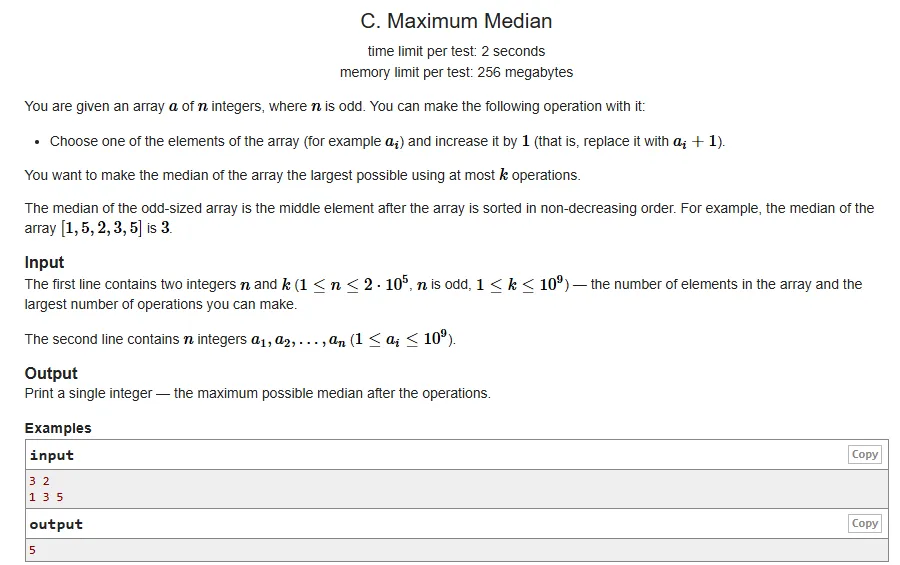
题目描述

给定一个包含n个整数的数组arr（n为奇数），可对其执行k次操作：选择数组中的任意一个元素，将其加1。要求执行k次操作后，使数组的中位数尽可能大。

约束条件

1 ≤ n ≤ 2 × 10^5，1 ≤ k ≤ 10^9，且n为奇数。

解题思路

1. 中位数定义：先将数组按升序排序，此时数组的中位数为排序后中间位置的元素（索引为(n-1)/2，0-based）。

2. 关键观察：要将当前中位数提升至x，需保证数组中所有大于等于当前中位数的元素，在操作后仍大于等于新中位数x。

例如：排序数组[1,1,2,3,4,4,5,5,6,8,8]的当前中位数为4，若要将中位数提升至6，需将4加2，并将两个5均加1（最终变为6）。

3. 核心逻辑：要将中位数提升至x，需将数组后半部分（从中位数位置开始到末尾）的所有元素提升至至少x。由于“提升中位数所需的操作次数”随x的增大而单调递增，因此可通过二分查找寻找最大可能的x。

4. 检查函数：对于给定的x，计算将中位数提升至x所需的操作次数，公式为：

$\sum_{i=(n+1)/2}^{n} \max(0, x - \texttt{arr}[i])$

（注：此处索引为1-based，若为0-based则起始索引为n//2）

若该操作次数≤k，则x是可行的（返回true）；否则不可行（返回false）。

C++实现

#include <bits/stdc++.h>
using namespace std;

int last_true(int lo, int hi, function<bool(int)> f) {
    lo--;
    while (lo < hi) {
        int mid = lo + (hi - lo + 1) / 2;
        if (f(mid)) {
            lo = mid;
        } else {
            hi = mid - 1;
        }
    }
    return lo;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int n, k;
    cin >> n >> k;
    vector<int> arr(n);
    for (int i = 0; i < n; i++) {
        cin >> arr[i];
    }
    sort(arr.begin(), arr.end());

    // 二分查找的边界：最小可能值为原中位数，最大可能值为原中位数 + k（极端情况：仅提升中位数一个元素）
    int lo = arr[n / 2];
    int hi = arr[n / 2] + k;

    // 定义检查函数（lambda表达式）
    auto is_possible = [&](int x) -> bool {
        long long ops = 0;  // 操作次数可能超过int范围，需用long long
        for (int i = n / 2; i < n; i++) {
            if (arr[i] < x) {
                ops += x - arr[i];
            }
            if (ops > k) {  // 提前终止，避免不必要的计算
                return false;
            }
        }
        return ops <= k;
    };

    cout << last_true(lo, hi, is_possible) << endl;
    return 0;
}

此处检查函数通过lambda表达式实现。

6. 常见错误（Common Mistakes）

错误1 - 差一错误（Off By One）

参考CSAcademy“函数二分查找”中的代码示例：

long long f(int x) { return (long long)x * x; }

int sqrt(int x) {
    int lo = 0;
    int hi = x;
    while (lo < hi) {
        int mid = (lo + hi) / 2;  // 中点向下取整
        if (f(mid) <= x) {
            lo = mid;
        } else {
            hi = mid - 1;
        }
    }
    return lo;
}

问题：当lo = 0且hi = 1时，会陷入无限循环。

计算mid = (0 + 1) / 2 = 0；
若x ≥ 0（如x = 1），则f(0) = 0 ≤ 1，执行lo = 0；
循环条件lo < hi（0 < 1）始终成立，导致无限循环。

解决方案：将中点计算方式改为向上取整，即mid = (lo + hi + 1) / 2。

错误2 - 未考虑负边界（Not Accounting for Negative Bounds）

考虑对firstTrue函数的轻微修改版本：

#include <functional>
using namespace std;

int first_true(int lo, int hi, function<bool(int)> f) {
    hi++;
    while (lo < hi) {
        int mid = (lo + hi) / 2;  // 对负整数除法时，结果会向上取整（而非向下取整）
        if (f(mid)) {
            hi = mid;
        } else {
            lo = mid + 1;
        }
    }
    return lo;
}

问题：当lo为负数时，该代码可能失效。例如：

int main() {
    // 期望输出-11（因区间[-10,-10]内无满足f(x)=true的x，应返回hi+1 = -10 + 1 = -9？原文表述为“输出-8而非-9”，需以实际逻辑为准）
    cout << first_true(-10, -10, [](int x) { return false; }) << "\n";

    // 会陷入无限循环
    cout << first_true(-10, -10, [](int x) { return true; }) << "\n";
}

原因：在C++中，负整数除法会“向上取整”（如(-10 + (-9)) / 2 = (-19)/2 = -9，而非-10），导致中点计算错误，进而引发逻辑异常或无限循环。

解决方案：将中点计算方式改为mid = lo + (hi - lo) / 2，避免直接对lo + hi进行除法（该方式对正负整数均能实现向下取整）：

#include <functional>
using namespace std;

int first_true(int lo, int hi, function<bool(int)> f) {
    hi++;
    while (lo < hi) {
        int mid = lo + (hi - lo) / 2;  // 正确的中点计算方式
        if (f(mid)) {
            hi = mid;
        } else {
            lo = mid + 1;
        }
    }
    return lo;
}

错误3 - 整数溢出（Integer Overflow）

对于firstTrue的第一种实现（mid = (lo + hi) / 2）：若lo + hi的值超过int的最大值（INT_MAX），会发生整数溢出，导致中点计算错误。
对于firstTrue的第二种实现（mid = lo + (hi - lo) / 2）：若hi - lo的初始值超过INT_MAX，同样会发生溢出。

解决方案：将变量类型从int改为long long，扩大数值存储范围：

#include <functional>
using namespace std;

long long first_true(long long lo, long long hi, function<bool(long long)> f) {
    hi++;
    while (lo < hi) {
        long long mid = lo + (hi - lo) / 2;
        if (f(mid)) {
            hi = mid;
        } else {
            lo = mid + 1;
        }
    }
    return lo;
}

7. 练习题（Problems）

USACO 相关题目

状态（Status）	来源（Source）	题目名称（Problem Name）	难度（Difficulty）	标签（Tags）
-	白银级（Silver）	奶牛舞蹈表演（Cow Dance Show）	简单（Easy）	显示标签（Show Tags）：二分查找（Binary Search）、有序集合（Sorted Set）
-	白银级（Silver）	会议安排（Convention）	简单（Easy）	显示标签（Show Tags）：二分查找（Binary Search）、排序（Sorting）
-	白银级（Silver）	愤怒的奶牛（Angry Cows）	简单（Easy）	显示标签（Show Tags）：二分查找（Binary Search）、排序（Sorting）
-	白银级（Silver）	社交距离（Social Distancing）	中等（Normal）	显示标签（Show Tags）：二分查找（Binary Search）、排序（Sorting）
-	白银级（Silver）	面包店（Bakery）	困难（Hard）	显示标签（Show Tags）：二分查找（Binary Search）
-	黄金级（Gold）	愤怒的奶牛（Angry Cows）	困难（Hard）	显示标签（Show Tags）：双指针（2P）、二分查找（Binary Search）、贪心（Greedy）、排序（Sorting）
-	黄金级（Gold）	哦哞牛奶（OohMoo Milk）	困难（Hard）	显示标签（Show Tags）：二分查找（Binary Search）、排序（Sorting）
-	白银级（Silver）	贷款偿还（Loan Repayment）	极难（Very Hard）	显示标签（Show Tags）：二分查找（Binary Search）、平方根（Sqrt）
-	黄金级（Gold）	奶牛依赖（Cowdependence）	极难（Very Hard）	显示标签（Show Tags）：二分查找（Binary Search）、前缀和（Prefix Sums）、平方根（Sqrt）、双指针（Two Pointers）
-	铂金级（Platinum）	负载均衡（Load Balancing）	疯狂（Insane）	显示标签（Show Tags）：二分查找（Binary Search）、排序（Sorting）

通用题目（General）

状态（Status）	来源（Source）	题目名称（Problem Name）	难度（Difficulty）	标签（Tags）
-	CSES	工厂机器（Factory Machines）	简单（Easy）	显示标签（Show Tags）：二分查找（Binary Search）
-	CSES	数组分割（Array Division）	简单（Easy）	显示标签（Show Tags）：二分查找（Binary Search）
-	CF（Codeforces）	猜第k个零（简单版）（Guess the K-th Zero (Easy)）	简单（Easy）	显示标签（Show Tags）：二分查找（Binary Search）
-	CF（Codeforces）	马哈茂德与伊哈布和函数（Mahmoud & Ehab & Function）	中等（Normal）	显示标签（Show Tags）：二分查找（Binary Search）
-	CC（CodeChef）	旅行奇妙（TripTastic）	中等（Normal）	显示标签（Show Tags）：二维前缀和（2D Prefix Sums）、二分查找（Binary Search）
-	CSES	乘法表（Multiplication Table）	中等（Normal）	显示标签（Show Tags）：二分查找（Binary Search）
-	CF（Codeforces）	教育场C题：魔法船（Edu C: Magic Ship）	中等（Normal）	显示标签（Show Tags）：二分查找（Binary Search）、前缀和（Prefix Sums）
-	CF（Codeforces）	会面地点无法更改（The Meeting Place Cannot Be Changed）	中等（Normal）	-
-	CF（Codeforces）	为归并排序做准备（Preparing for Merge Sort）	中等（Normal）	显示标签（Show Tags）：二分查找（Binary Search）
-	CF（Codeforces）	最小化差值（Minimizing Difference）	中等（Normal）	显示标签（Show Tags）：二分查找（Binary Search）、贪心（Greedy）、前缀和（Prefix Sums）
-	CF（Codeforces）	阿马尔的漂亮数组（Ammar-utiful Array）	中等（Normal）	显示标签（Show Tags）：二分查找（Binary Search）、前缀和（Prefix Sums）
-	AC（AtCoder）	握手（Handshake）	困难（Hard）	显示标签（Show Tags）：二分查找（Binary Search）、前缀和（Prefix Sums）、排序（Sorting）
-	CF（Codeforces）	最大中位数（Max Median）	困难（Hard）	显示标签（Show Tags）：二分查找（Binary Search）、前缀和（Prefix Sums）
-	CF（Codeforces）	分组车厢（Grouped Carriages）	困难（Hard）	显示标签（Show Tags）：二分查找（Binary Search）、优先队列（Priority Queue）
-	CF（Codeforces）	吃豆人（Packmen）	困难（Hard）	-
-	CF（Codeforces）	关卡生成（Level Generation）	困难（Hard）	-
-	Baltic OI（波罗的海信息学奥林匹克）	2012 - 移动设备（Mobile）	极难（Very Hard）	显示标签（Show Tags）：二分查找（Binary Search）、栈（Stack）

8. 小测验（Quiz）

对于以下代码，在大小为n的有序数组中查找某个数字时，其最坏情况和最好情况的时间复杂度分别是多少？

bool binary_search(int x, std::vector<int> &a) {
    int l = 0;
    int r = a.size() - 1;
    while (l < r) {
        int m = (l + r) / 2;
        if (a[m] == x) {
            return true;
        } else if (x > a[m]) {
            l = m + 1;
        } else {
            r = m - 1;
        }
    }
    return false;
}

1. $\Theta(\log n)$ / $\Theta(\log n)$

2. $\Theta(\log n)$ / $\Theta(1)$

3. $\Theta(n)$ / $\Theta(\log n)$

4. $\Theta(\log n)$ / $\Theta(\log \log n)$

答案解析：

最好情况：第一次二分就找到目标值x（即a[m] == x），此时仅需1次迭代，时间复杂度为$\Theta(1)$；
最坏情况：需将搜索区间缩小至1个元素后才能确定是否存在x，共需$\log_2 n$次迭代，时间复杂度为$\Theta(\log n)$。

因此正确答案为选项2。