Two Pointers
双指针法(Two Pointers)
通过在数组中遍历两个具有单调性的指针,以线性时间寻找满足特定条件的索引对。
编程语言:C++
前置知识:青铜级(Bronze)- 排序入门(Introduction to Sorting)
目录
参考资料(Resources)
双指针法(Two Pointers)
解决方案 - 书籍问题(Solution - Books)
代码实现(Implementation)
练习题(Problems)
小测验(Quiz)
参考资料(Resources)
参考资料来源 | 章节/主题 | 内容说明 |
|---|---|---|
CPH | 8.1 - 双指针法(Two Pointers) | 上述问题的解决方案 |
IUSACO | 14.1 - 双指针法(Two Pointers) | 上述内容 + 最大子数组和相关提及 |
CF EDU | 双指针法(Two Pointers Method) | 双指针法的视频讲解 |
双指针法(Two Pointers)
双指针法通过在数组中遍历两个指针来追踪一个区间的起始和结束位置。正如CPH(注:可能指《Competitive Programming 3》)中求解“两数之和(2SUM)”问题的方案所示,该方法也可用于追踪数组中的两个值。
书籍问题(Books)
难度:CF - 简单(Easy)
重点问题——在继续学习前,请尽力解决这个问题!
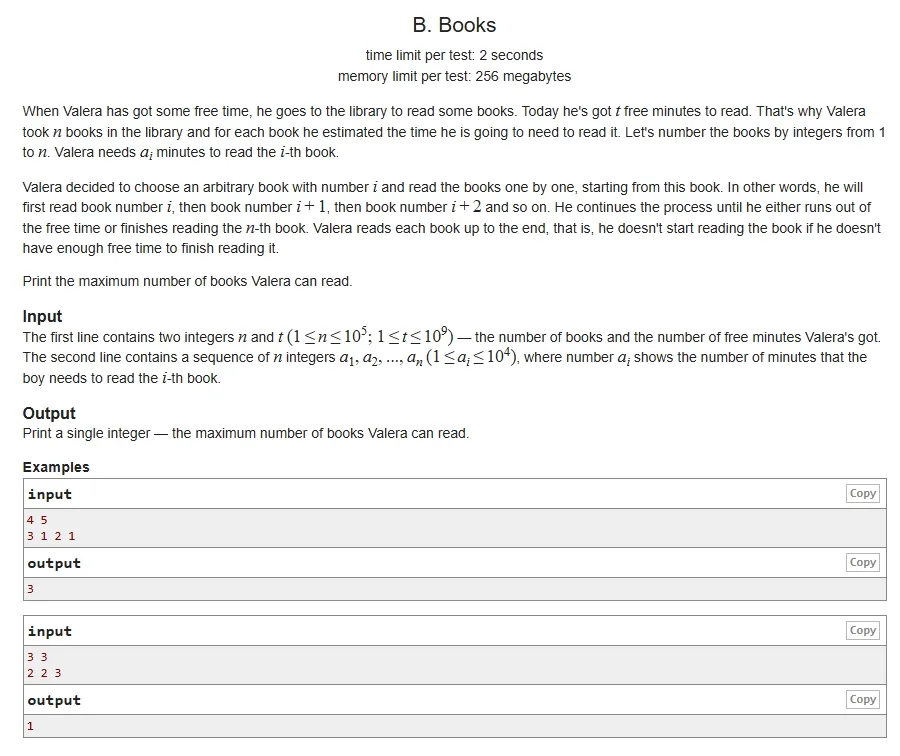
https://codeforces.com/contest/279/problem/B
解决方案 - 书籍问题(Solution - Books)
我们需要找出在*t*分钟内可以读完的最长连续书籍片段。
为实现这一目标,我们可以定义left和right两个指针,分别表示片段的起始和结束位置。初始时,两个指针都位于数组的起始处。这两个变量之所以被称为“指针”,正是“双指针法”名称的由来。
对于每个递增的left值,我们不断移动right指针,直到当前片段的总阅读时间达到最大且不超过*t*为止。
ans变量用于存储迄今为止我们遇到的最大片段长度,其计算方式为right - left + 1(片段中书籍的数量)。
当left指针向右移动一位后,当前片段的总阅读时间会减少,因此right指针永远不需要向左移动。由此可得出:
由于两个指针最多各移动*N*(数组长度)次,因此该算法的总体时间复杂度为$\mathcal{O}(N)$。
以下为示例,我们以样例输入中的第一个案例来演示:
左指针(Left Pointer) | left | |||
|---|---|---|---|---|
${arr}[i]$ | 3 | 1 | 2 | 1 |
右指针(Right Pointer) | right |
第一步:我们可将右指针移动到索引1的位置:
左指针(Left Pointer) | left | |||
|---|---|---|---|---|
${arr}[i]$ | 3 | 1 | 2 | 1 |
右指针(Right Pointer) | right |
此时,该区间内数值的和为4,包含2个数值(书籍)。因此,当前的最大片段长度ans更新为2。
第二步:将左指针向右移动1位,此时需从总和中减去左指针移动前指向的数值3,新的总和变为1。数组状态如下:
左指针(Left Pointer) | left | |||
|---|---|---|---|---|
${arr}[i]$ | 3 | 1 | 2 | 1 |
右指针(Right Pointer) | right |
第三步:现在我们可以将右指针移动到数组的末尾(索引3)。此时区间内数值的和为$1+2+1=4$,片段长度为3。因此,ans更新为3。
左指针(Left Pointer) | left | |||
|---|---|---|---|---|
$texttt{arr}[i]$ | 3 | 1 | 2 | 1 |
右指针(Right Pointer) | right |
由于右指针已到达数组末尾,整个过程至此结束。最终得到的最大片段长度ans为3。
https://usaco.guide/animations/two_pointers.mp4
实用技巧(Pro Tip)
在这个问题中,你可以将这两个指针理解为在维护一个“滑动窗口”(sliding window),用于表示当前正在考虑的书籍片段。
代码实现(Implementation)
时间复杂度:$\mathcal{O}(N)$
#include <bits/stdc++.h>
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int N, T;
cin >> N >> T;
vector<int> A(N);
for (int &a : A) cin >> a;
int r = -1, sum = 0, ans = 0;
// sum stores sum of A[l ... r inclusive]
for (int l = 0; l < N; sum -= A[l++]) {
while (r + 1 < N && sum + A[r + 1] <= T) sum += A[++r];
ans = max(ans, r - l + 1);
}
cout << ans << "\n";
}练习题(Problems)
状态(Status) | 来源(Source) | 题目名称(Problem Name) | 难度(Difficulty) | 标签(Tags) |
|---|---|---|---|---|
CSES | 两数之和(Sum of Two Values) | 简单(Easy) | 双指针(2P)、排序(Sorting) | |
CSES | 子数组和 I(Subarray Sums I) | 简单(Easy) | 滑动窗口(Sliding Window) | |
CSES | 三数之和(Sum of Three Values) | 简单(Easy) | 双指针(2P)、排序(Sorting) | |
白银级(Silver) | 配对(Paired Up) | 简单(Easy) | 双指针(2P)、排序(Sorting) | |
CF(Codeforces) | 蜂窝网络(Cellular Network) | 简单(Easy) | 双指针(2P)、二分查找(Binary Search) | |
CF(Codeforces) | 它们无处不在(They Are Everywhere) | 简单(Easy) | 双指针(2P) | |
CF(Codeforces) | 测验大师(Quiz Master) | 中等(Normal) | 双指针(2P)、滑动窗口(Sliding Window)、排序(Sorting) | |
白银级(Silver) | 钻石收集者(Diamond Collector) | 中等(Normal) | 双指针(2P)、排序(Sorting) | |
白银级(Silver) | 嗜睡的牧牛(Sleepy Cow Herding) | 中等(Normal) | 双指针(2P)、排序(Sorting) | |
CF(Codeforces) | 热烈的情感循环(An impassioned circulation of affection) | 中等(Normal) | 双指针(2P) | |
白银级(Silver) | 奶牛体检(Cow Checkups) | 中等(Normal) | 双指针(Two Pointers) |
小测验(Quiz)
双指针算法是什么?
1. 追踪两个索引以寻找满足特定条件的子数组。
2. 追踪两个索引以寻找满足特定条件的索引对。
3. 一种以$\mathcal{O}(1)$时间回答区间和查询的方法。
4. 一种分治算法,将数组分成两半以高效寻找满足特定条件的元素。