Logic Gates

Logic gates
Electronic circuits in computers, many memories and controlling devices are made up of thousands of logic gates.
Logic gates take binary inputs and produce a binary output.
Several logic gates combined together form a logic circuit and these circuits are designed to carry out a specific function.
The checking of the output from a logic gate or logic circuit can be done using a truth table.
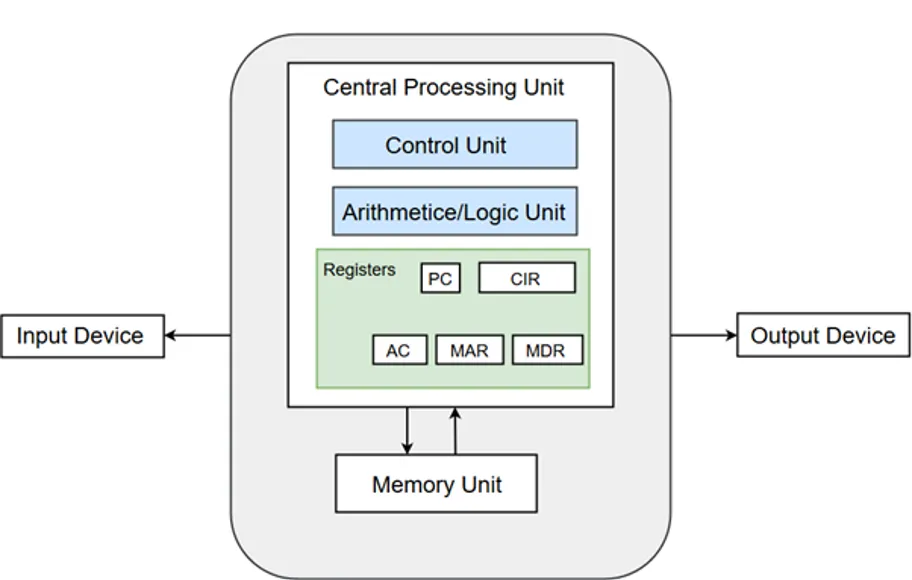
NOT gate
Description
The output, X, is 1 if the input A is NOT 1
How to write this
X = NOT A (logic notation)
$X = \overline{A}$ (Boolean algebra)
Truth table
Input | Output |
|---|---|
A | X |
0 | 1 |
1 | 0 |
AND gate
Description
The output, X, is 1 if input A is 1 and input B is 1
How to write this
X = A AND B (logic notation)
$X = {A \cdot B}$ (Boolean algebra)
Truth table
Input | Input | Output |
|---|---|---|
A | B | X |
0 | 0 | 0 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
OR gate
Description
The output, X, is 1 if input A is 1 or input B is 1.
How to write this
X = A OR B (logic notation)
$X = A + B$ (Boolean algebra)
Truth table
Input | Input | Output |
|---|---|---|
A | B | X |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 1 |
NAND gate
Description
The output, X, is 1 if input A is NOT 1 or input B is NOT 1.
How to write this
X = A NAND B (logic notation)
$X = \overline{A \cdot B}$ (Boolean algebra)
Truth table
Input | Input | Output |
|---|---|---|
A | B | X |
0 | 0 | 1 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
NOR gate
Description
The output, X, is 1 if: input A is NOT 1 and input B is NOT 1
How to write this
X = A NOR B (logic notation)
$X = \overline{A + B}$ (Boolean algebra)
Truth table
Input | Input | Output |
|---|---|---|
A | B | X |
0 | 0 | 1 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 0 |
XOR gate
Description
The output, X, is 1 if (input A is 1 AND input B is NOT 1) OR (input A is NOT 1 AND input B is 1)
How to write this
X = A XOR B (logic notation)
$X = ({A \cdot \overline{B}}) + ({\overline{A} \cdot B})$ (Boolean algebra)
(Note: this is sometimes written as: $(A + B) \cdot \overline{(A \cdot B )}$)
Truth table
Input | Input | Output |
|---|---|---|
A | B | X |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
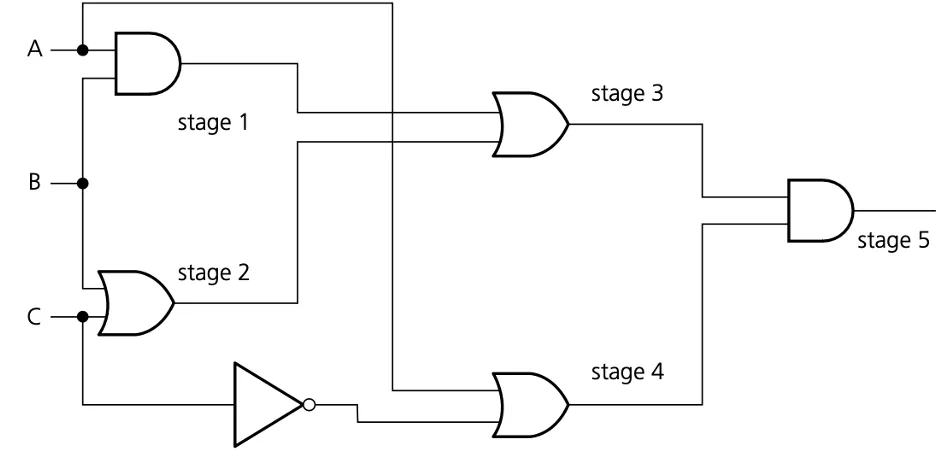
Logic circuits 1
Produce a truth table for the following logic circuit
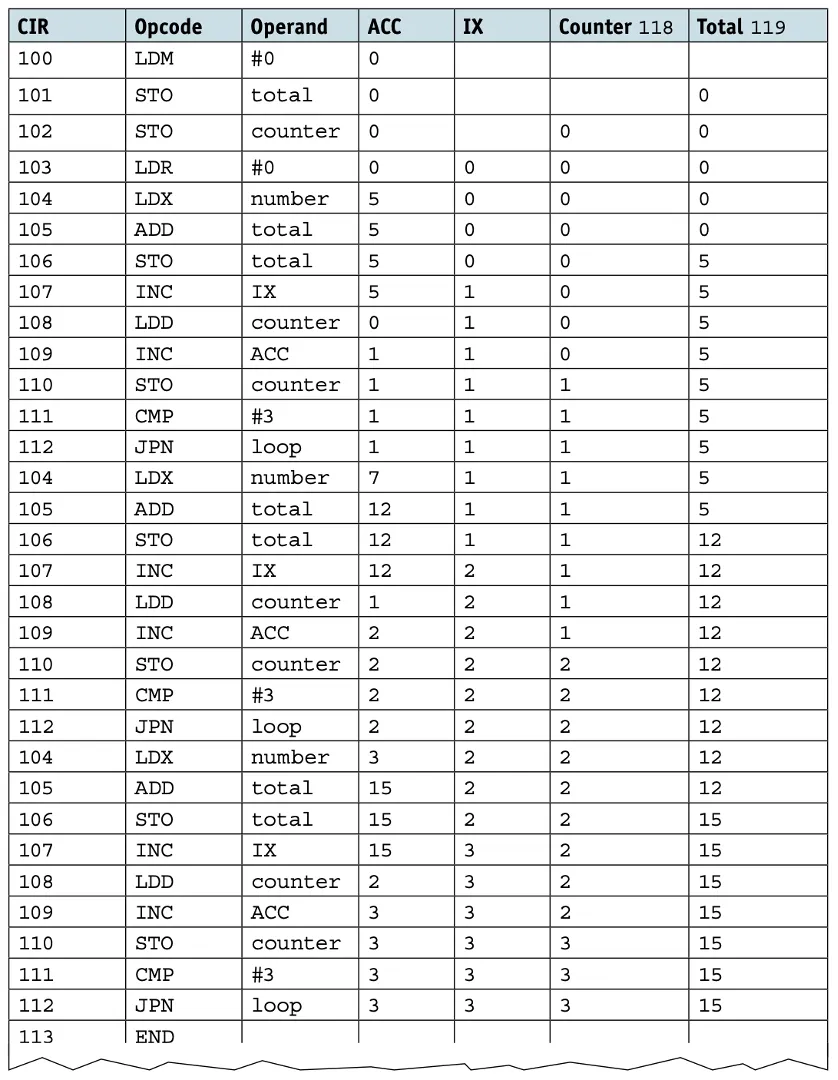 |
|---|
 |
 |
 |
 |
Complete the truth table for the logic circuit.
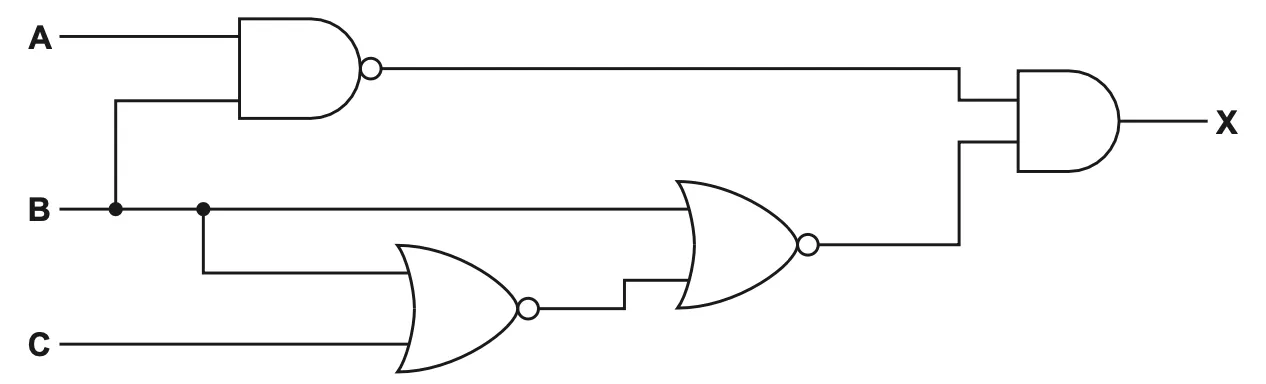
A | B | C | X |
|---|---|---|---|
0 | 0 | 0 | |
0 | 0 | 1 | |
0 | 1 | 0 | |
0 | 1 | 1 | |
1 | 0 | 0 | |
1 | 0 | 1 | |
1 | 1 | 0 | |
1 | 1 | 1 |
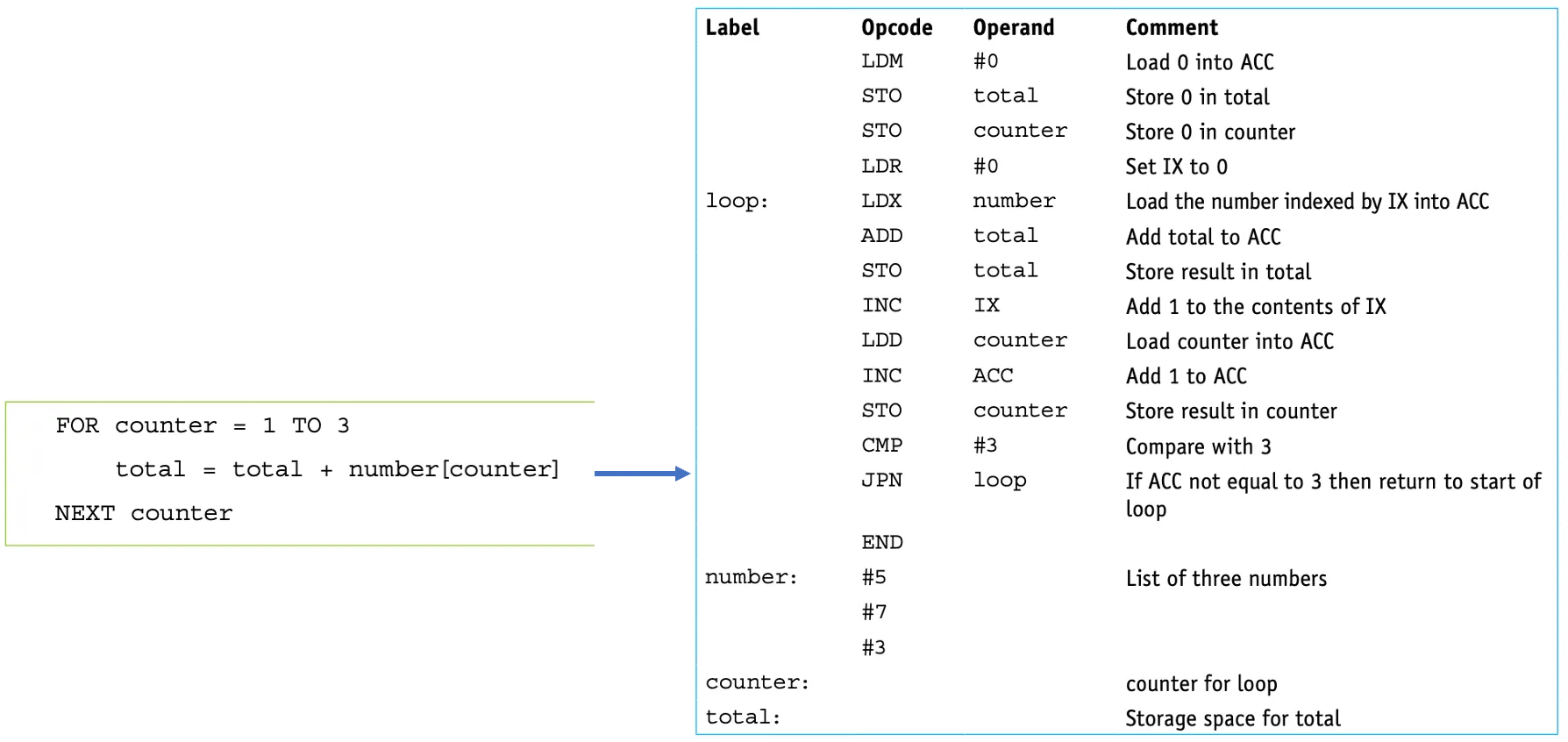
Logic circuits 2
A safety system uses three inputs to a logic circuit. An alarm, X, sounds if input A represents ON and input B represents OFF, or if input B represents ON and input C represents OFF.
Produce a logic circuit and truth table to show the conditions which cause the output X to be 1.
X = 1 if (A = 1 AND B = NOT 1) OR (B = 1 AND C = NOT 1)
this equates to A is ON and B is OFF
this equates to B is ON AND C is OFF
$X = ({A \cdot \overline{B}}) + ({B} \cdot \overline{C})$
 |
|---|
 |
 |
Draw the logic circuit for the logic expression:
X = (A AND B) OR (NOT ((A AND C) AND (B OR C))).
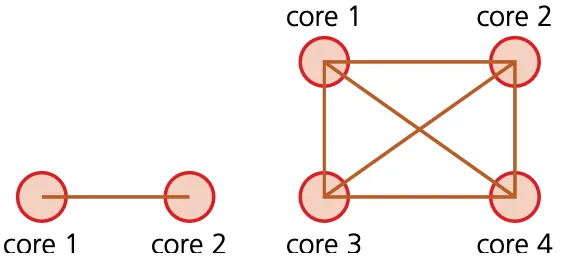
Logic circuits 3
A wind turbine has a safety system which uses three inputs to a logic circuit. A certain combination of conditions results in an output, X, from the logic circuit being equal to 1. When the value of X = 1, the wind turbine is shut down.
either turbine speed ≤ 1000 rpm and bearing temperature > 80 °C
or turbine speed > 1000 rpm and wind velocity > 120 kph
or bearing temperature ≤ 80 °C and wind velocity > 120 kph
The following table shows which parameters are being monitored and form the three inputs to the logic circuit.
The output, X, will have a value of 1 if any of the following combination of conditions occur:
Parameter description | Parameter | Binary value | Description of condition |
|---|---|---|---|
turbine speed | S | 0 | turbine speed ≤ 1000 rpm |
turbine speed | S | 1 | turbine speed > 1000 rpm |
bearing temperature | T | 0 | bearing temperature ≤ 80 °C |
bearing temperature | T | 1 | bearing temperature > 80 °C |
wind velocity | W | 0 | wind velocity ≤ 120 kph |
wind velocity | W | 1 | wind velocity > 120 kph |
1. turbine speed 1000 rpm and bearing temperature > 80 °C logic statement:
(S = NOT 1 AND T = 1)
2. turbine speed > 1000 rpm and wind velocity > 120 kph logic statement:
(S = 1 AND W = 1)
3. bearing temperature 80 °C and wind velocity > 120 kph logic statement:
(T = NOT 1 AND W = 1)
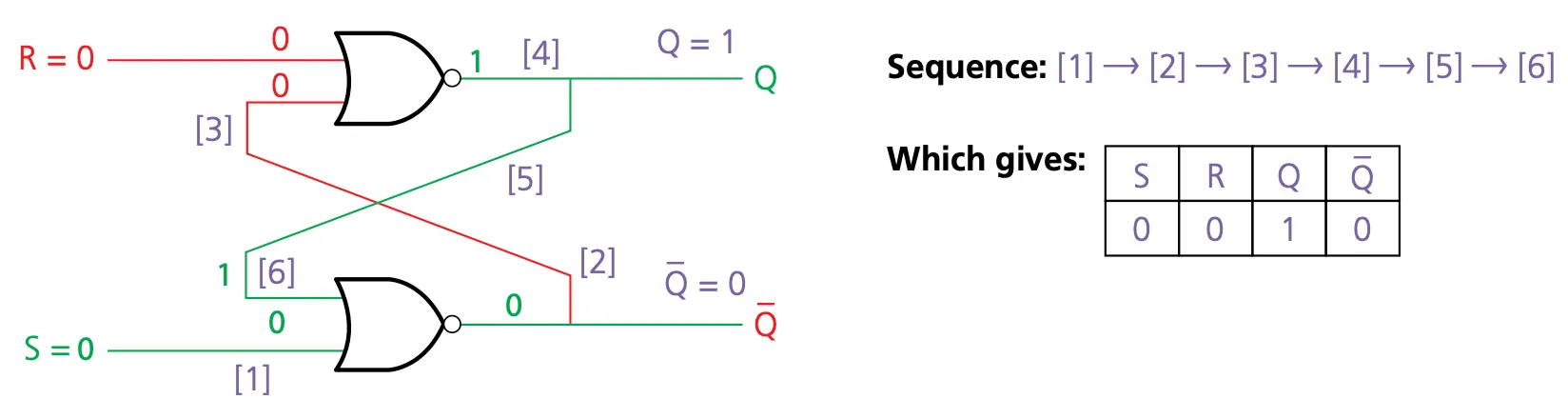 |
|---|
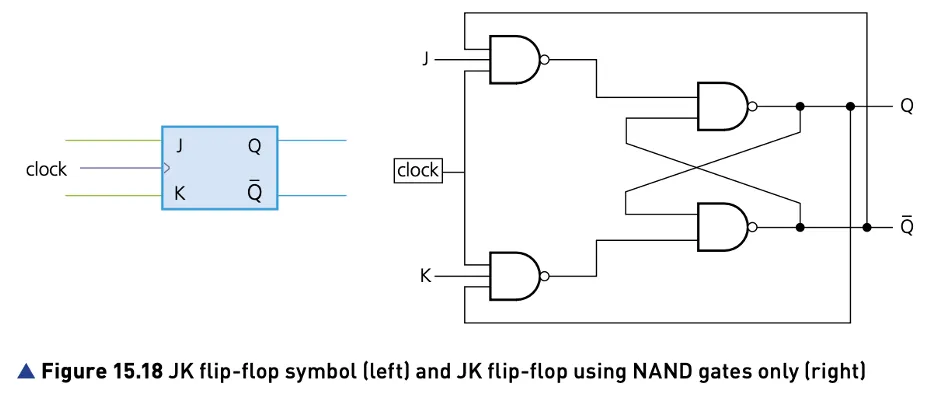 |
 |
 |
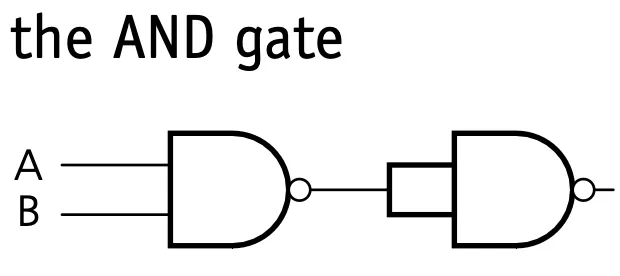
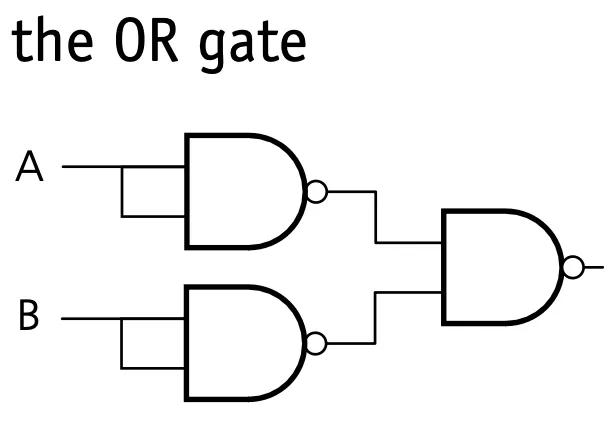
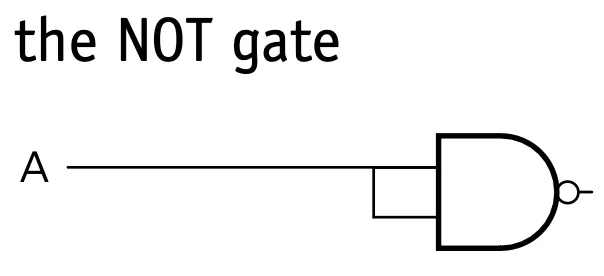
Logic circuits in the real world
AND gate
OR gate
NOT gate
Multi-input logic gates
Multi-input AND gates
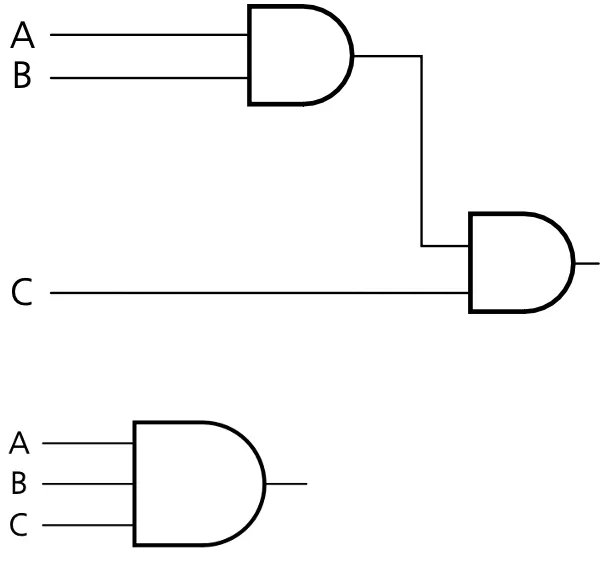
A | B | C | A.B.C |
|---|---|---|---|
0 | 0 | 0 | 0 |
0 | 0 | 1 | 0 |
0 | 1 | 0 | 0 |
0 | 1 | 1 | 0 |
1 | 0 | 0 | 0 |
1 | 0 | 1 | 0 |
1 | 1 | 0 | 0 |
1 | 1 | 1 | 1 |
Multi-input OR gates
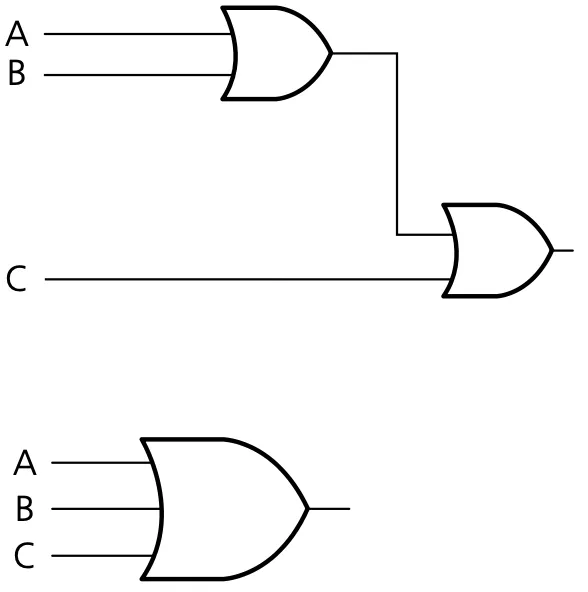
A | B | C | A + B + C |
|---|---|---|---|
0 | 0 | 0 | 0 |
0 | 0 | 1 | 1 |
0 | 1 | 0 | 1 |
0 | 1 | 1 | 1 |
1 | 0 | 0 | 1 |
1 | 0 | 1 | 1 |
1 | 1 | 0 | 1 |
1 | 1 | 1 | 1 |