Number Systems

Understand binary

• Any form of data needs to be converted to binary to be processed by a computer.

• The basic building block in all computers is the binary number system.

Switch

Switch ON is 1 and OFF is 0.

Digit weight

• Every one of us is used to the decimal or denary (base 10) number system. This uses the digits 0 to 9 which are placed in ‘weighted’ columns.

• Example: 3x10000 + 1x1000 + 4x100 + 2x10 + 1x1 = 31421

Binary to denary

• Except for denary, we use binary(base 2) and hexadecimal(base 16) number system in the computer.

• The binary system uses 1s and 0s only which gives these corresponding weightings.

• We can convert binary number to denary according to digit weightings.

• Example: 1110 11102 = 128 + 64 + 32 + 8 + 4 + 2 = 23810

Hexadecimal to denary

• The hexadecimal system is very closely related to the binary system.

• Hexadecimal is a base 16 system.

• Because it is a system based on 16 different digits, the numbers 0 to 9 and the letters A to F are used to represent hexadecimal digits.

• A = 10, B = 11, C = 12, D = 13, E = 14 and F = 15.

• We can convert hexadecimal number to denary according to digit weightings.

Example: 0112316 = 1x4096 + 1x256 + 2x16 + 3x1 = 438710

Use of the hexadecimal system

• Areas within computer science that hexadecimal is used should be identified:

  • Error codes

  • MAC addresses

  • IPv6 addresses

  • HTML colour codes

• Hexadecimal is easier for humans to understand than binary, as it is a shorter representation of the binary.

• When the memory contents are output to a printer or monitor, this is known as a memory dump.

Denary to binary

• Converting from denary to binary is slightly more complex.

• This method involves successive division by 2 until the result is 0; the remainders are then written from bottom to top to give the binary value.

• Example: 10710 = 110 10112

Denary to hexadecimal

• Converting from denary to hexadecimal is slightly similar with denary to binary.

• This method involves successive division by 16; the remainders are then written from bottom to top to give the hexadecimal value.

• Example: 200410 = 7D416

Binary to hexadecimal

• Since 16 = 24, four binary digits are equivalent to each hexadecimal digit.

• Example: $1111100001_2 = 0011\ 1110\ 0001_2 = 3E1_{16}$

Hexadecimal to binary

• Since 16 = 24, one hexadecimal digit are equivalent to four binary digits.

• Example: 45A16 = 0100 0101 10102

Binary addition

bianry addtion

• 0 + 0 = 0

• 1 + 0 = 1 (sum 1 and carry 0)

• 1 + 1 = 10 (sum 0 and carry 1 )

• 1 + 1 + (carry 1) = 11= sum 1 and carry 1

• Add 0 0 1 0 0 1 0 1 (37 in denary) and 0 0 1 1 1 0 1 0 (58 in denary).

• The sum is 0101 1111, which is 95 in denary.

Overflow error

• Add 0 1 0 1 0 0 1 0 (82 in denary) and 0 1 0 0 0 1 0 1 (69 in denary).

• The sum is 1001 0111, which is -105 (Incorrect)

Overflow error

• The expected answer for 82 + 69 is 151, which is out of range for the 8 bits register (-128~127), this is known as an overflow error.

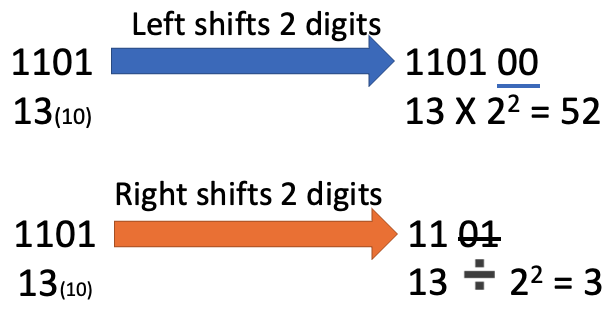
Logical shifts

• The positive binary integer is multiplied or divided according to the shift performed.

• Bits shifted from the end of the register are lost and zeros are shifted in at the opposite end of the register.

• The most significant bit(s) or least significant bit(s) are lost.